Thema: Bildregistrierung
Für die Diagnose und Behandlung müssen häufig mehrere Röntgen-, CT- oder MRT-Aufnahmen verglichen werden. Beispielsweise möchte man wissen, ob eine Therapie erfolgreich war und die Tumore tatsächlich entfernt wurden. Dies wird heutzutage in der Regel von Radiologen durchgeführt, die von Hand die 3D-Bilddaten Schicht für Schicht vergleichen. Am Institute for Mathematics and Image Computing (MIC) wird an Verfahren geforscht, die den Radiologen diese aufwändige Arbeit erleichtern.
Theoretisch müssen dabei nur die Bilddaten voneinander subtrahiert werden, so dass die Unterschiede zu sehen sind. Leider funktioniert dies aber nicht, wie an folgendem Beispiel zu sehen ist:


Da die Aufnahmen in der Regel in einem Abstand von mehreren Wochen bis Monaten gemacht werden, enthalten die Daten noch einige andere Änderungen: Die Patienten lagen nicht gleich im Gerät, haben Gewicht verloren, die Aufnahme wurde an einer anderen Position des Atemzyklus gemacht oder Organe haben sich leicht gegeneinander verschoben.
Um nur die relevanten Änderungen zu erkennen, müssen diese unerwünschten Bewegungen korrigiert werden. Es wird also eine Funktion, das sogenannte Deformationsfeld, gesucht, die zu jedem Bildpunkt im ersten (Vorher-) Bild den korrespondierenden Punkt im zweiten (Nachher-) Bild angibt.
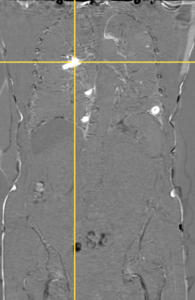
So können dann die Bewegungen über Interpolationsverfahren rückgängig gemacht werden und das Differenzbild zeigt klar, an welchen Stellen sich relevante Änderungen ergeben haben, in diesem Fall im Bereich der Lunge:
Basierend auf dem Deformationsfeld können dem Radiologen weitere Werkzeuge zur Verfügung gestellt werden, wie beispielsweise eine Cursorsynchronisation, die bei einem Klick in eines der Bilder die entsprechende Position im anderen Bild markiert. Damit kann beispielsweise schnell überprüft werden, ob kleine Gewebeveränderungen bereits in der früheren Aufnahme vorhanden waren oder neu entstanden sind.

Bildregistrierung als Optimierungsproblem
Wie findet man solch ein Deformationsfeld nur anhand zweier Aufnahmen? Mathematisch lässt sich dieses Problem als Optimierungsproblem formulieren: Die Eingabedaten sowie weiteres Vorwissen werden in ein Zielfunktion verpackt, die mögliche Deformationsfelder bewertet. Mit entsprechenden Optimierungsalgorithmen wird dann ein Deformationsfeld gesucht, das bezüglich dieser Zielfunktion optimal ist, d.h. für das diese den kleinsten Funktionswert annimmt. Diese Probleme sind sehr hochdimensional – häufig zehntausende bis mehrere Millionen Variablen, haben viele „falsche“ (lokale) Minima oder besitzen keine klassische Ableitung, auf der aktuelle Optimierungsverfahren in der Regel aufbauen.
Die folgende interaktive Demo zeigt ein einfaches starres (Rotation/Translation) Registrierungsverfahren für zwei Gewebeschnitte. Der Startpunkt kann per Drag & Drop oder per Touch verschoben werden, zu sehen ist dann, wie das Optimierungsverfahren die Bewegung schrittweise korrigiert.
