Bachelorarbeiten
Am Ende des ersten Studienabschnitts steht die Bachelorarbeit. Darin wird ein Thema nach wissenschaftlichen Grundsätzen aufgearbeitet und manchmal auch schon ein neuer Satz bewiesen oder ein neues Verfahren ausprobiert. In der Regel entsteht eine Bachelorarbeit über 6 Monate. Hier ein paar Beispiele, die an den Mathematikinstituten entstanden sind:
Lizzie Neumann: Mathematische Populationsmodelle
Eine wichtige Fragestellung der mathematischen Biologie ist, wie sich Populationen – Bevölkerungen, Raub- und Beutetiere oder auch Krankheitserreger – langfristig entwickeln und wie dies von den äußeren Bedingungen abhängt. Lizzie hat drei Ansätze verglichen, um das Verhalten vorherzusagen, insbesondere wenn sich die Populationen gegenseitig beeinflussen.
Felix Kastner: Bildrekonstruktion mit nichtparametrischen Rauschmodellen
Viele Probleme in der medizinischen (und nichtmedizinischen!) Bildverarbeitung sind sogenannte Inverse Probleme: Von den Messdaten – zum Beispiel Magnetresonanz- oder Computertomographie-Rohdaten – soll auf die unbekannten Bilddaten geschlossen werden; allerdings hat man nur ein gutes mathematisches Modell, das den umgekehrten Prozess – von den Bilddaten zu den Messungen – beschreibt. Wenn bekannt ist, welcher Wahrscheinlichkeitsverteilung das Rauschen folgt, lassen sich trotzdem häufig stabile Rekonstruktionsverfahren finden. Felix hat einen mathematischen Ansatz entwickelt, der mit sehr wenig Vorwissen über das Rauschen auskommt: Es genügt, eine untere und obere Schranke anzugeben. Das ermöglicht es, Bilddaten zuverlässig zu verarbeiten, auch wenn man praktisch keine Informationen über das Aufnahmeverfahren hat.


Björn-Hergen Lebs: Vermeidung des Overfittings von Random Forests
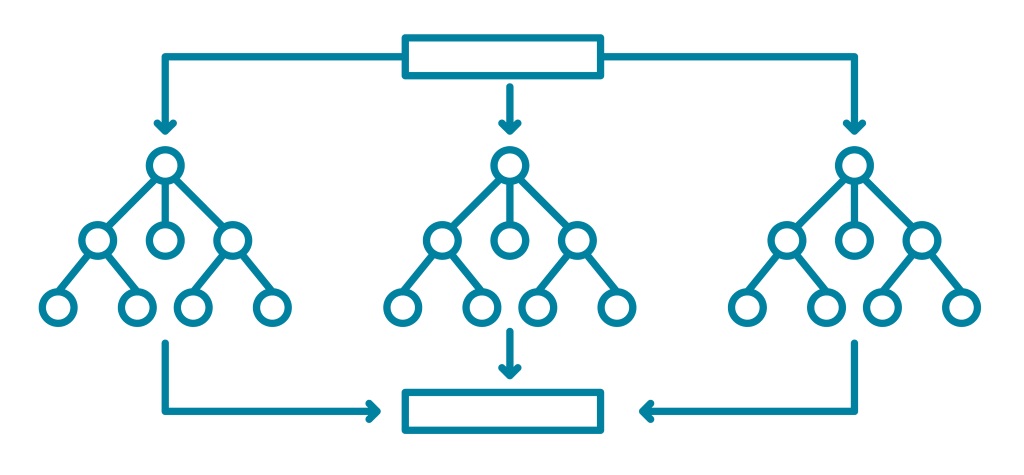
Random Forests sind eine beliebte Methode des maschinellen Lernen (Künstliche Intelligenz), um beispielsweise aus vorliegenden Patientendaten eine automatische Diagnose zu erzeugen. Dabei wird durch die Kombination der Vorhersage vieler einzelner Entscheidungsbäume eine gemeinsame, bessere Vorhersage getroffen. Wie die meisten maschinellen Lernverfahren neigen auch Random Forests zum Overfitting (Überanpassung). Dass heißt, dass sie die Trainigsdaten „auswendig“ lernen, ohne die eigentlich wichtigen Zusammenhänge abzubilden. Björn-Hergen hat untersucht, ob dieses Overfitting mittels Pruning, also dem Zurückschneiden der einzelnen Entscheidungsbäume, vermieden werden kann, um so mit weniger Daten genauere Vorhersagen treffen zu können.
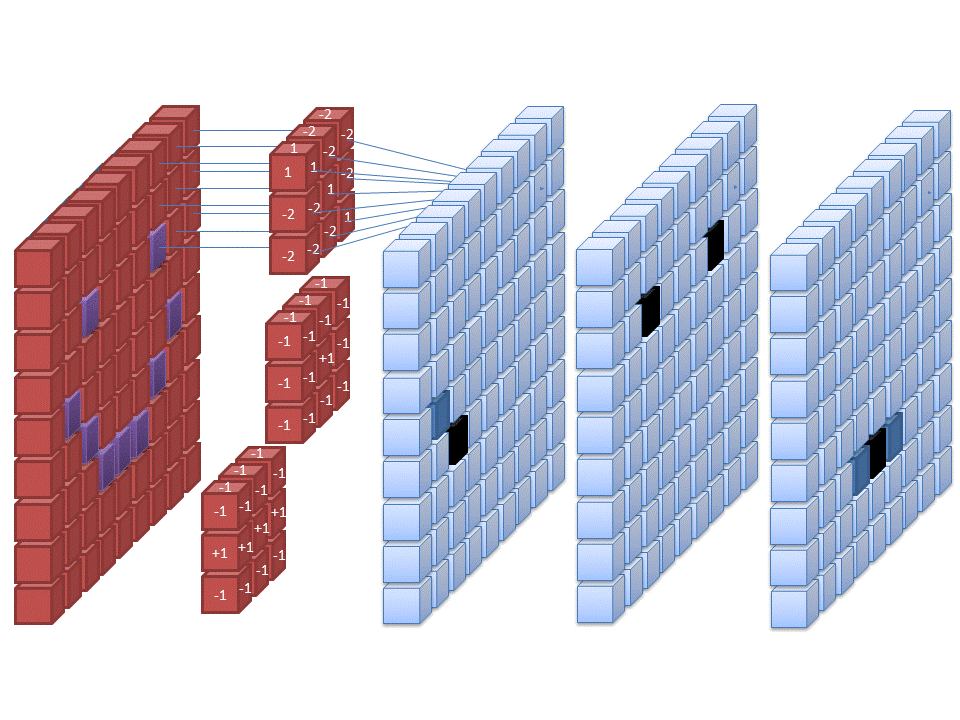
Aktuelle Verfahren für die künstliche Intelligenz, zum Beispiele um Objekte in Bildern zu erkennen oder zur Spracherkennung, basieren auf Netzwerken aus unterschiedlichen linearen und nichtlinearen Funktionen, deren Parameter so angepasst („trainiert“) werden, dass sie die Aufgabe lösen. Ein großer Durchbruch war dabei die Einführung sogenannter Residualnetzwerke, die größere Netzwerke mit mehr Schichten ermöglichen. Christian hat untersucht, wie sich das Training solcher Residualnetzwerke in Verbindung bringen lässt mit einem klassischen mathematischen Problem: der Optimierung auf einem Funktionenraum, d.h. der Suche nach einer optimalen Funktion. Durch die Verbindung lassen sich bekannte Ergebnisse auf die neuen Lernverfahren übertragen, zum Beispiel wie man größere/mächtigere Netzwerke konstruieren kann, die sich trotzdem noch gut trainieren lassen.
Masterarbeiten
Die Masterarbeit ist der krönende Abschluss des Studiums: Hier wird ein Thema deutlich tiefer als in der Bachelorarbeit behandelt, das Schreiben einer Masterarbeit dauert in der Regel 6 Monate Vollzeit. Häufig entstehen dabei auch Ergebnisse, die später in wissenschaftlichen Zeitschriften veröffentlich werden.
Christina Schmitz: Vergleich deterministischer und stochastischer Neuronenmodelle
Das nach den Nobelpreisträgern benannte Hodgkin-Huxley-Modell beschreibt präzise, wie Signale in Neuronen weitergeleitet werden. Allerdings ist das Modell aufwändig und damit schwierig zu simulieren und zu analysieren. Christina hat theoretisch und experimentell untersucht, wie gut sich dieses realistische aber aufwändige Modell mit einfacheren Modellen annähern lässt, die sich in der Praxis besser einsetzen lassen. Mathematisch gesehen handelt es sich dabei um Systeme nichtlinearer Differentialgleichungen, die eine Zufallskomponente in Form von (unbekanntem) Rauschen enthalten können, sogenannte stochastische Differentialgleichungen.
Kristin Haßelbusch: Variationelle quantitative Niederschlagsschätzung auf Grundlage von polarimetrischen Radardaten

Zur Erzeugung von Niederschlagskarten, zum Beispiel für „Regenradar“-Apps und zur Wettervorhersage, werden tatsächlich Radarsysteme eingesetzt: Die Menge der reflektierten Radarstrahlung gibt einen Aufschluss über die Dichte der Regenwolken und damit die aktuelle Niederschlagsmenge. Kristin hat untersucht, wie man diese Schätzung mit polarimetrischen Messungen verbessern kann. Dabei werden horiztontal und vertikal polarisierte Radarstrahlen verwenden, so dass man nicht nur Informationen über die Größe, sondern auch über die Form der Regentropfen bekommt und auch zwischen Regen und Hagel besser unterscheiden kann: Hagel sieht zum Beispiel im Durschnitt rund aus, Regentropfen werden im Fallen abgeflacht. Kristin hat dazu ein mathematisches Modell aufgestellt, um die Niederschlagsschätzung zu verbessern, und es mit Hilfe echter Niederschlagsmessungen überprüft.
In Kooperation mit hydro & meteo GmbH, Lübeck
Laura Schumann: Glaukom-Prognose anhand multivariater Daten
Manche Leute machen wiederholt Sehtests, um nötigenfalls mit einer Therapie zu beginnen, um bleibenden Schäden vorzubeugen. Die Prognose wird ungenauer, wenn die Blickrichtung nicht genau eingehalten wurde oder die Reaktionszeit variiert. Laura hat untersucht, wie man diese Probleme kompensieren kann, indem man die Korrelation berücksichtigt zwischen benachbarten Arealen des Gesichtsfeldes und Arealen, die mit denselben Nervenzellen verbunden sind. Auf die eine Weise erkennt man die Krankheit früher, auf die andere vermeidet man Fehlalarme.
Roland Haase: Low-rank- und sparsity-basierte Bildregistrierung
Wie trennt man in einer räumlich-zeitlichen Aufnahme des schlagenden Herzens die regelmäßige Bewegung (zum Beispiel die Bewegung des Herzens im Brustkorb) von der unregelmäßigen, also zu Beispiel dem turbulenten Blutfluss im inneren des Herzens? Roland hat dafür eine Methode entwickelt und implementiert, die die Bewegung in ihre wesentlichen Bestandteile zerlegen kann. Das übergeordnete Problem ist das der Bildregistrierung: Für eine Folge von Aufnahmen oder eine Videosequenz eines bewegten Objekts wird eine Funktion gesucht, die beschreibt, wie sich alle Strukturen im Bild – zum Beispiel eine Herzklappe – über die Zeit bewegen und deformieren. Das ist ein zentrales Problem der Bildverarbeitung und bei vielen bildbasierten medizinischen Studien der erste notwendige Schritt.
Laura Schumann: Glaukom-Prognose anhand multivariater Daten
Manche Leute benötigen wiederholt Sehtests, um festzustellen, ob mit einer Therapie begonnen werden muss, da sonst bleibende Schäden auftreten können. Die Prognose wird besser, wenn die Form der Kurve stimmt. Sie kann auch daneben liegen, weil die Blickrichtung bei den Sehtests nicht genau eingehalten wurde und weil die Reaktionszeit variiert. Laura hat sich damit beschäftigt, Das kann man nachbessern, indem man die Korrelation berücksichtigt zwischen benachbarten Arealen des Gesichtsfeldes und Arealen, die mit denselben Nervenzellen verbunden sind. Auf die eine Weise erkennt man die Krankheit früher, auf die andere vermeidet man Fehlalarme. Besonders spannend war für mich die Bearbeitung einer relevanten medizinischen Fragestellung und die dafür benötigte Einarbeitung in den medizinischen Kontext sowie die Vertiefung fortgeschrittener statistischer Methoden.

Bildmaterial: Cecbur, CC BY-SA 4.0 | Darin, PIC4U, Rudie, Shanvood, Vector/Adobe Stock | Eric Kurth, NOAA/NWS/ER/WFO/Sacramento
